

Dans ce mode de transmission, on définit la phase instantanée par :
qi(t) = 2p f0t + j(t)
| La fréquence instantanée s'écrit alors : Fi(t) = | 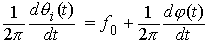 |
Le signal transmis par modulation angulaire s'écrit alors : x(t) = A cos[2p f0t + j(t)]
Expression d'un signal modulé en phase :
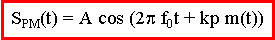
Représentation en Diagramme de Fresnel du signal modulé :

Fi(t) = f0 + DFi(t) =
f0 + kf m(t)
| On a également : Fi(t) = | 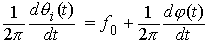 |
| Donc qi(t) = | 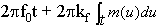 |
Expression d'un signal modulé en fréquence :

| SPM(t) = A cos(2p f0t + b cos(wmt)) |
| SFM(t) = A cos(2p f0t + b sin(wmt)) |
| Avec b = | 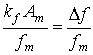 | : taux de modulation |
 |
 |
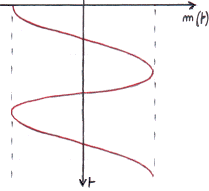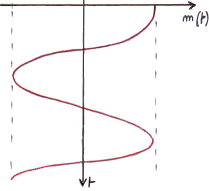 |
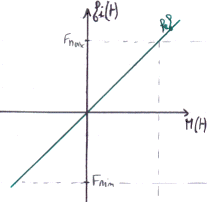
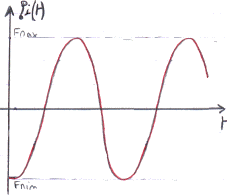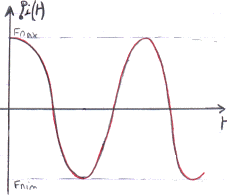
La fréquence instantanée Fi(t) est bien proportionnelle au signal modulant m(t),
avec
un coefficient kf . Donc, si le signal modulant m(t) est sinusoïdal,
Fi(t) est également sinusoïdale, de même phase, mais d'amplitude dépendant de
kf.
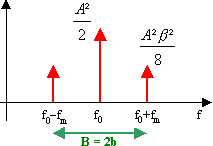
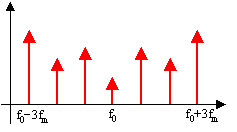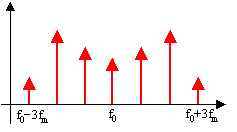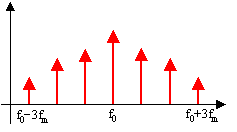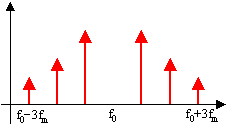
De plus, le spectre s'élargi au fur et à mesure que b
augmente.
En effet, les raies situées au fréquences f0
± n fm apparaissent
progressivement
et il y aura d'autant plus de raies d'amplitude significative que
b sera grand.
On peut démontrer que 98% de la puissance du signal est transmis dans la bande utile B
comportant ces raies significatives.
Le problème consiste à définir le nombre de ces raies.
On note N(b) le nombre de raies significatives,
la largeur de la bande utile B est :
Règle de Carson :
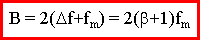
| Où b = |  |
est le taux de modulation |
L'inconvénient de cette méthode réside dans le fait qu'elle exige des dispositifs d'asservissements de la fréquence porteuse délicats à mettre en oeuvre.

L'oscillateur produisant la porteuse est complètement isolé du reste du système et
peut être facilement stabilisé en fréquence à l'aide d'un quartz.
D'autre part, si l'on désire effectuer une modulation de phase, plutôt qu'une modulation
de fréquence, il suffit d'éliminer l'intégrateur.
L'inconvénient de cette méthode réside dans le fait qu'elle exige des multiplieurs de fréquence large bande difficile à réaliser.
Le filtre doit présenter une atténuation (ou gain) linéaire en fonction de la fréquence sur la bande B du signal modulé. En général, on utilise la pente de la fonction de transfert du circuit résonant.
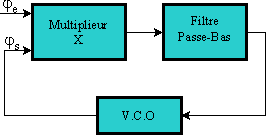
Le multiplieur de la PLL est un comparateur de phase : sa tension de sortie est
proportionnelle à l'écart de phase entre les deux signaux qui lui sont appliqués.
Le filtre passe-bas assure le filtrage du signal à la sortie du comparateur de phase
et il intervient dans la fonction globale du système, permettant de maîtriser les
performances de la boucle. Le V.C.O (Voltage Control Oscillator) est un oscillateur
commandé en tension :
il fournit un signal d'amplitude constante dont la fréquence
varie proportionellement à la tension injectée.